多层感知机

2 minute read

Published: September 21, 2021

本文详细介绍了从感知机到多层感知机（MLP）的演变历程，分析了 XOR 问题对 AI 发展的影响及非线性激活函数的重要性。文章深入讲解了 MLP 的结构、常用激活函数（Sigmoid、Tanh、ReLU）及基于 PyTorch 的代码实现，并探讨了参数初始化、深层网络优势及“维度灾难”等核心问题。

🎦 本节课程视频地址 👇

感知机（Perceptron）

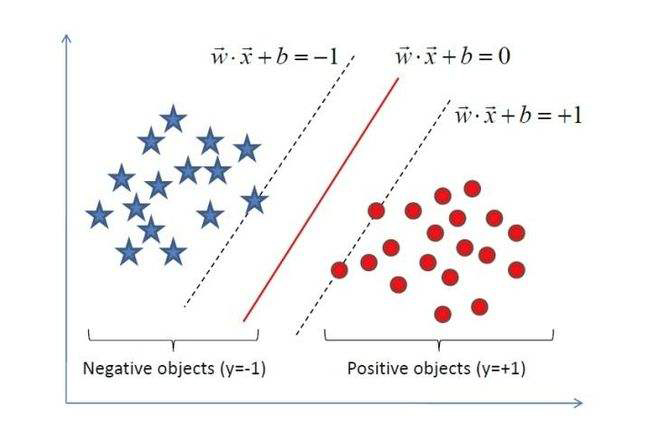
最早的 AI 模型之一，相当于单层神经网络。给定输入向量$\mathbf{x}$，权重向量$\mathbf{w}$，和偏移$b$，感知机输出：

\[o=\sigma(\langle{\mathbf{w}},{\mathbf{x}}\rangle+b)\] \[\sigma(x)= \begin{cases} 1& \text{if x>0} \\ 0& \text{otherwise} \end{cases}\]

二分类：感知机输出离散的两类
- VS 线性回归：输出实数；
- VS Softmax 回归：输出置信度；
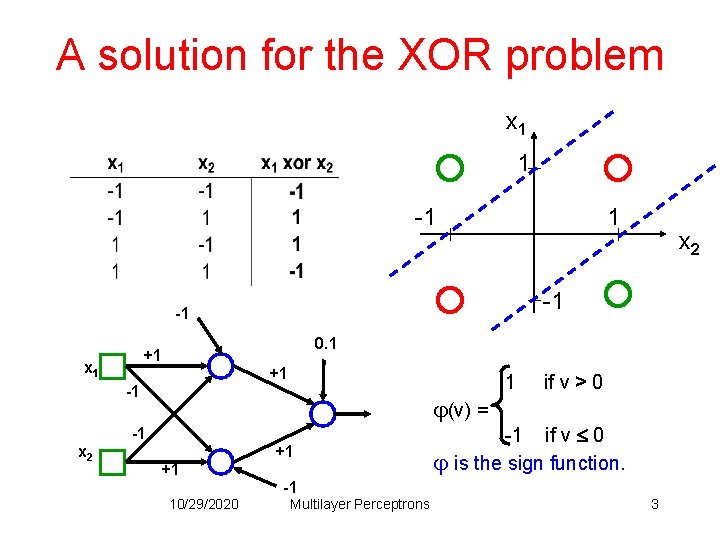
如何训练感知机

initialize w=0 and b=0
repeat
    if y_i[<w,x_i>+b] <= 0 then:
        w <- w + y_i·x_i and b <- b + y_i
    end if
until all classified correctly

等价于使用批量大小为 1 的梯度下降，并使用如下的损失函数

把每一个样本单独带入更新梯度。

感知机收敛定理
- 数据在半径$r$内
- 余量$\rho$分类两类
  \[y(\mathbf{x}^T\mathbf{w}+b)\ge\rho, \rho>0\]
- 对于$\Vert\mathbf{w}\Vert^2+b^2\le1$，感知机保证在$\frac{r^2+1}{\rho^2}$步后收敛。

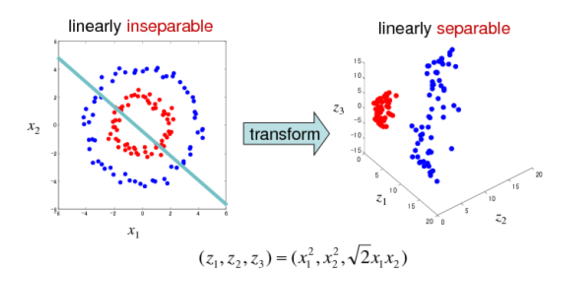
XOR 问题(Minsky&Papert,1969)

计算机科学家Marvin Minsky（后世人们称他为：人工智能之父）和 Seymour Papert 在其 1969 年的书《感知器》（Perceptrons）中提供了单层人工网络无法执行 XOR 的证据。

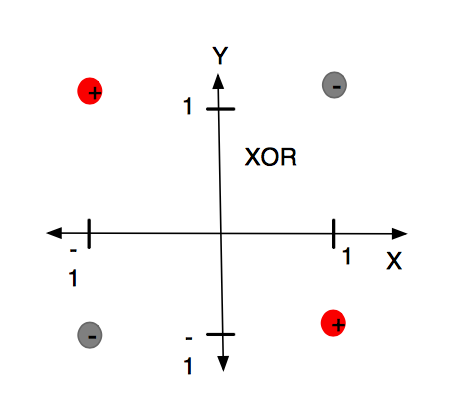
因为感知机的分割面是线性的，在上图中不管怎么做，都无法画出一条线可以完美分类红灰两种类别。这个结论是如此令人震惊，以至于许多计算机科学家将其归咎于神经网络研究在 1980 年代前的持续低迷状态，因此造成了第一次 AI 寒冬。

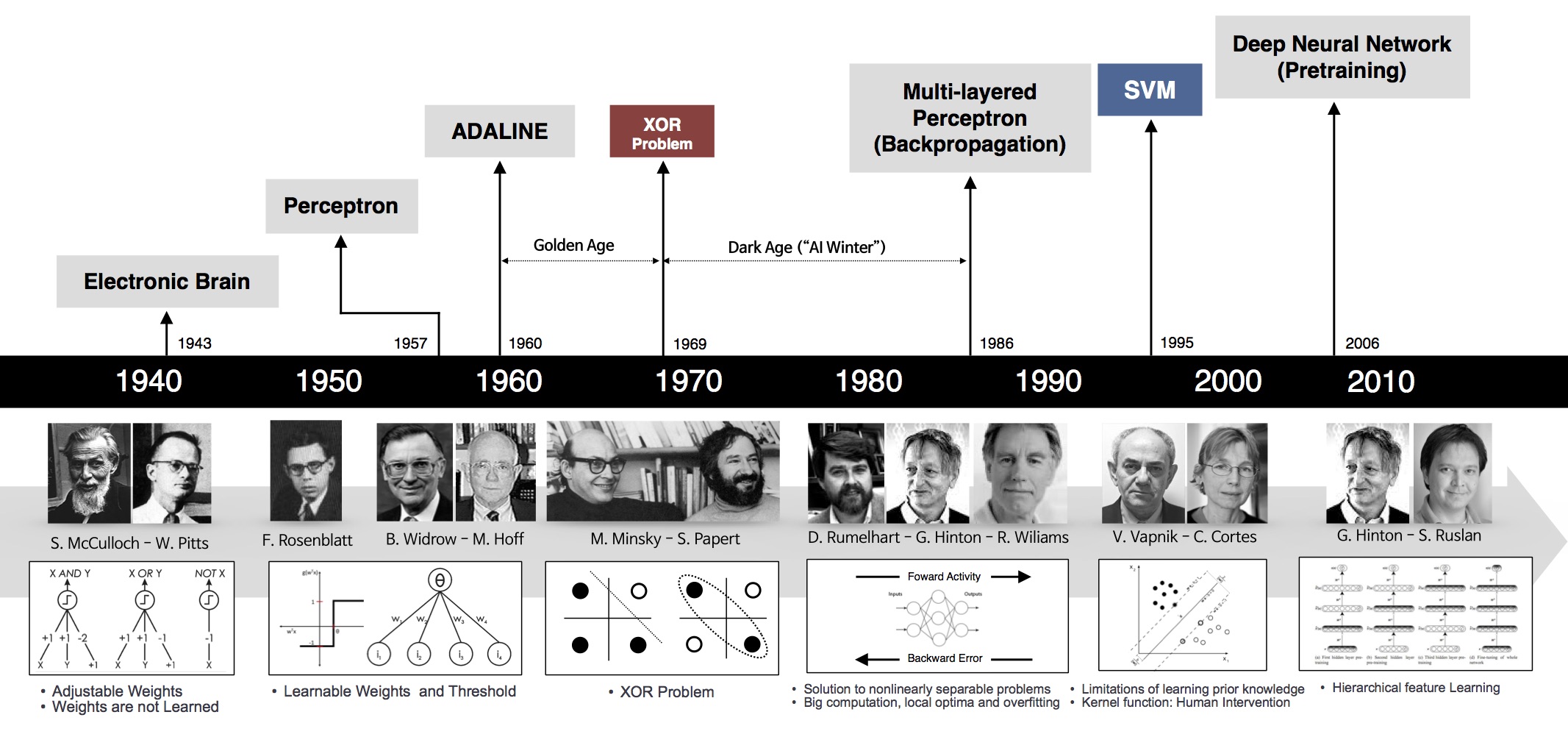
后来引入非线性激活函数（如“核方法”、“支持向量机（SVM）”等）、多层感知机后，对特征空间进行非线性扭曲变换，才使 XOR 之类问题转换为线性可分问题得以解决。

注：柏林洪堡大学等机构的研究者在 2020 年的研究证实，人类皮层上层中发现的一种新型电信号，皮层神经元树突臂中的微小区室每个都可以执行数学逻辑上的复杂操作，而不是像之前人们所认为的需要多层神经网络。例如连感知机都搞不定的异或运算，单个神经元即可轻松解决。其论文“Dendritic action potentials and computation in human layer 2/3 cortical neurons”刊登在《Science》，引发了广泛的关注。

多层感知机(MLP)

既然一层学不了，就用简单函数的组合，层层嵌套，解决问题。

单隐藏层——单分类

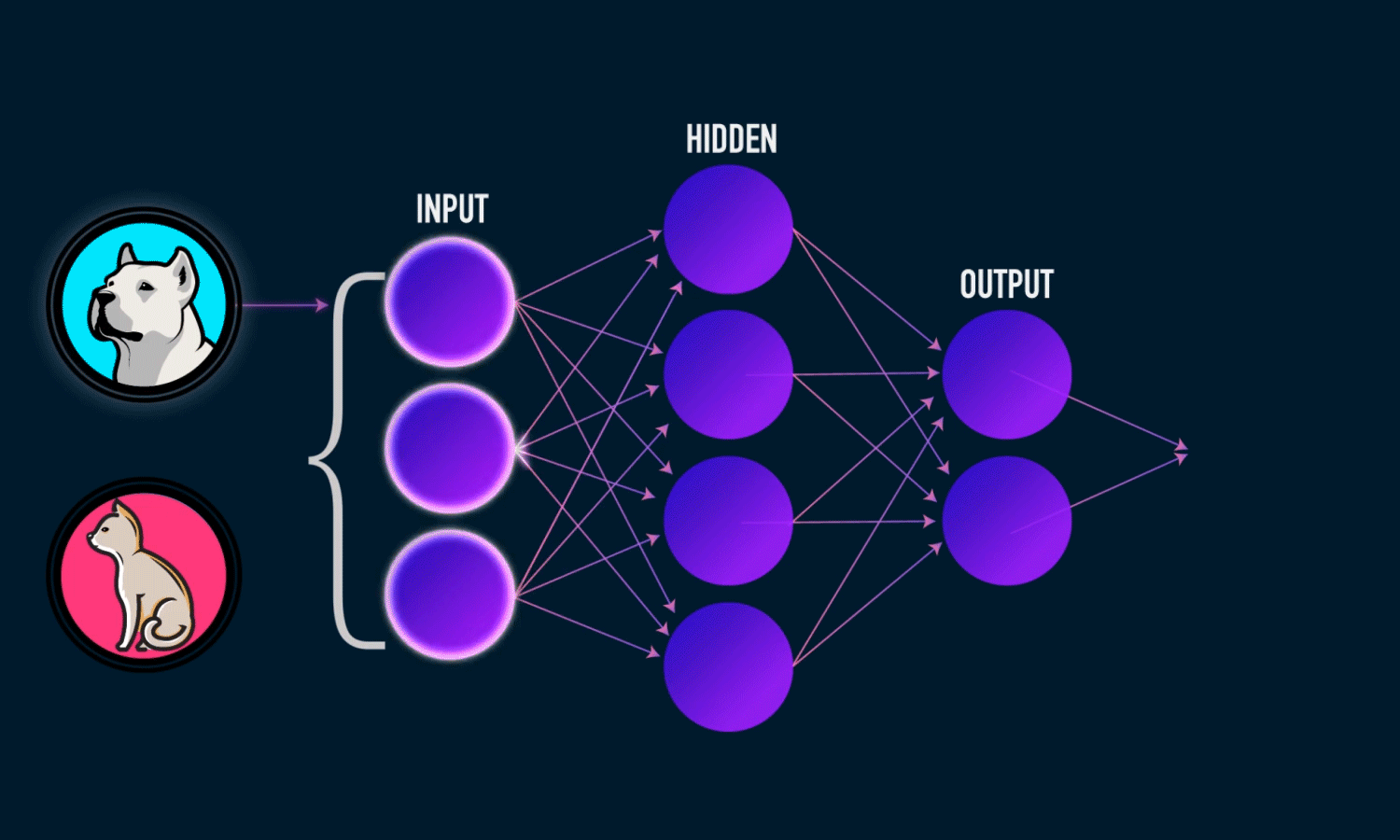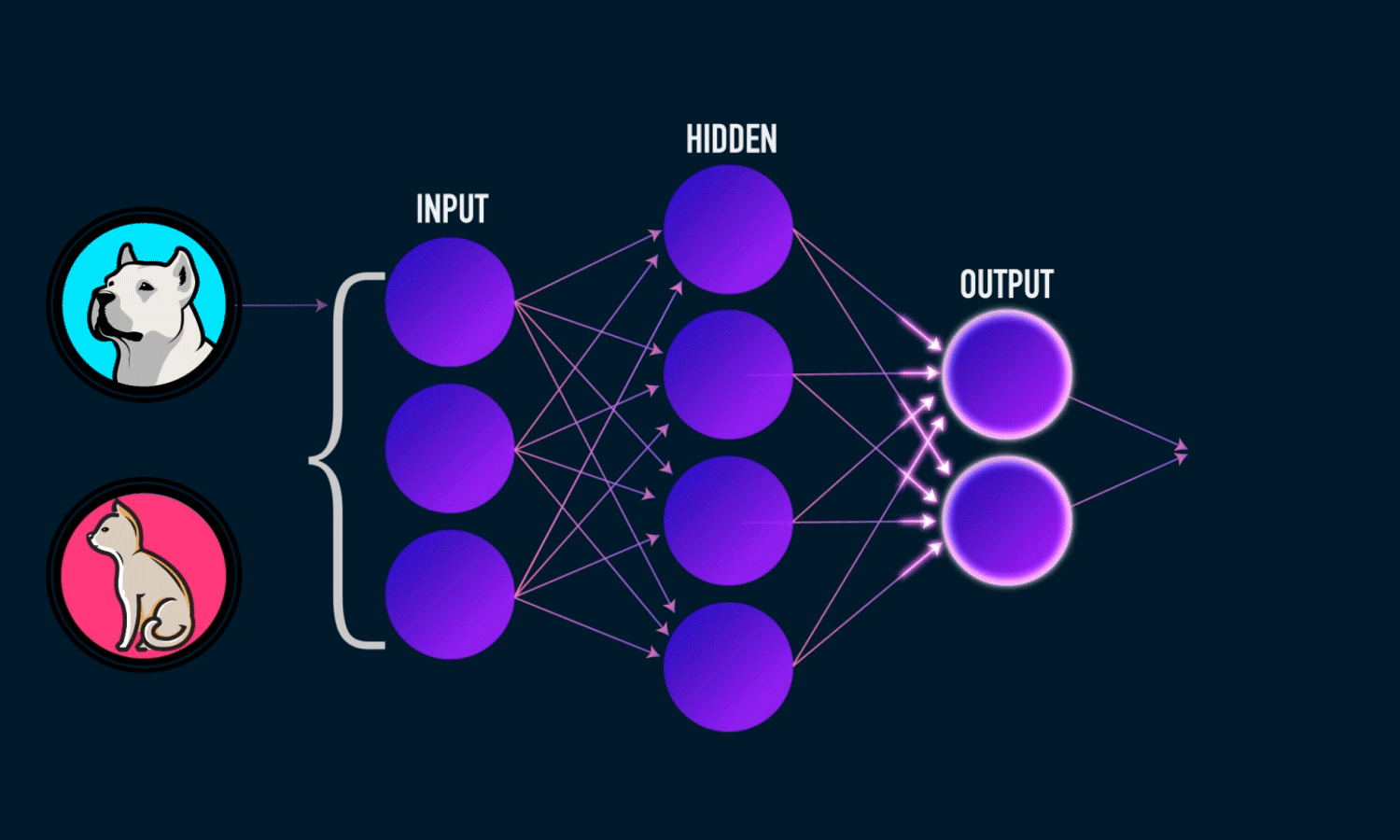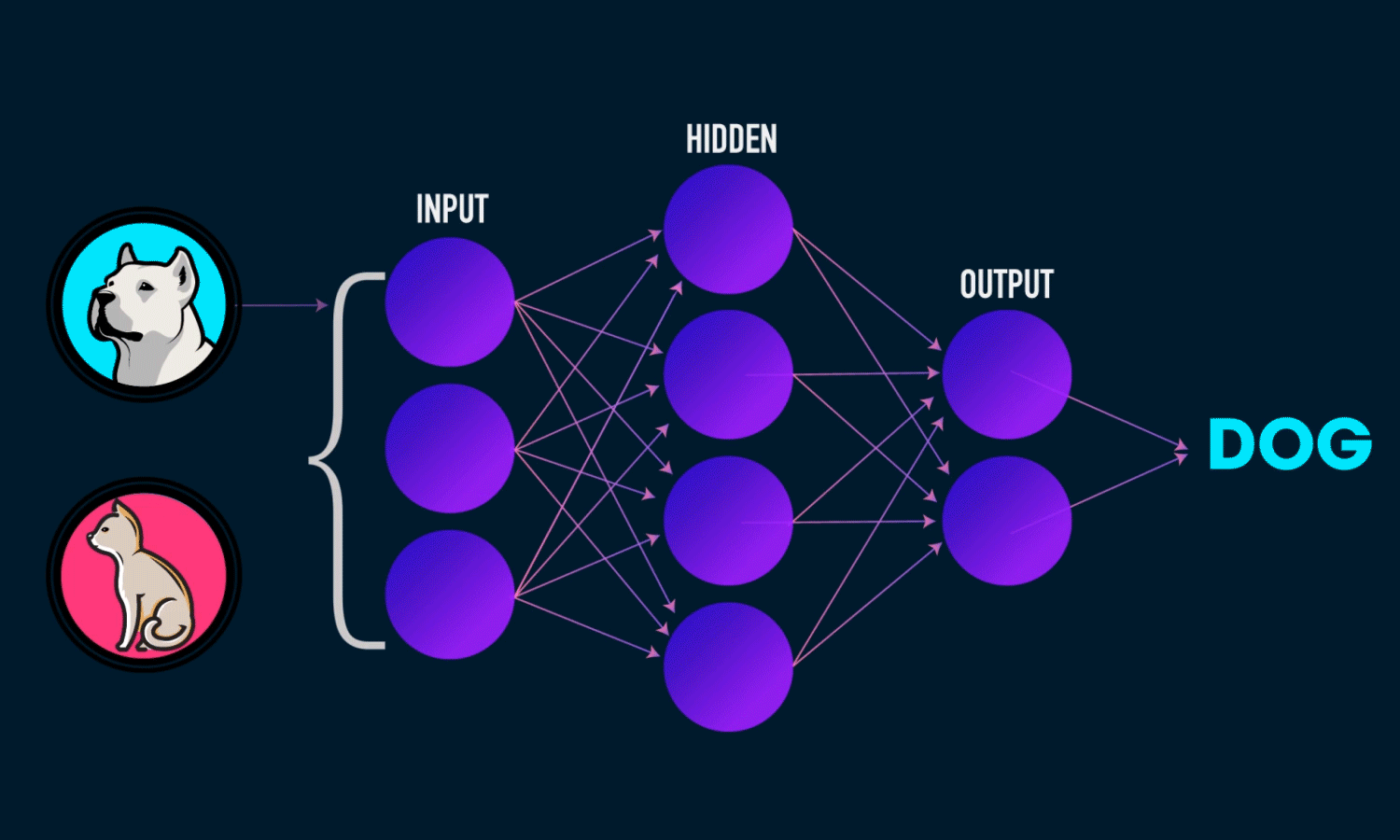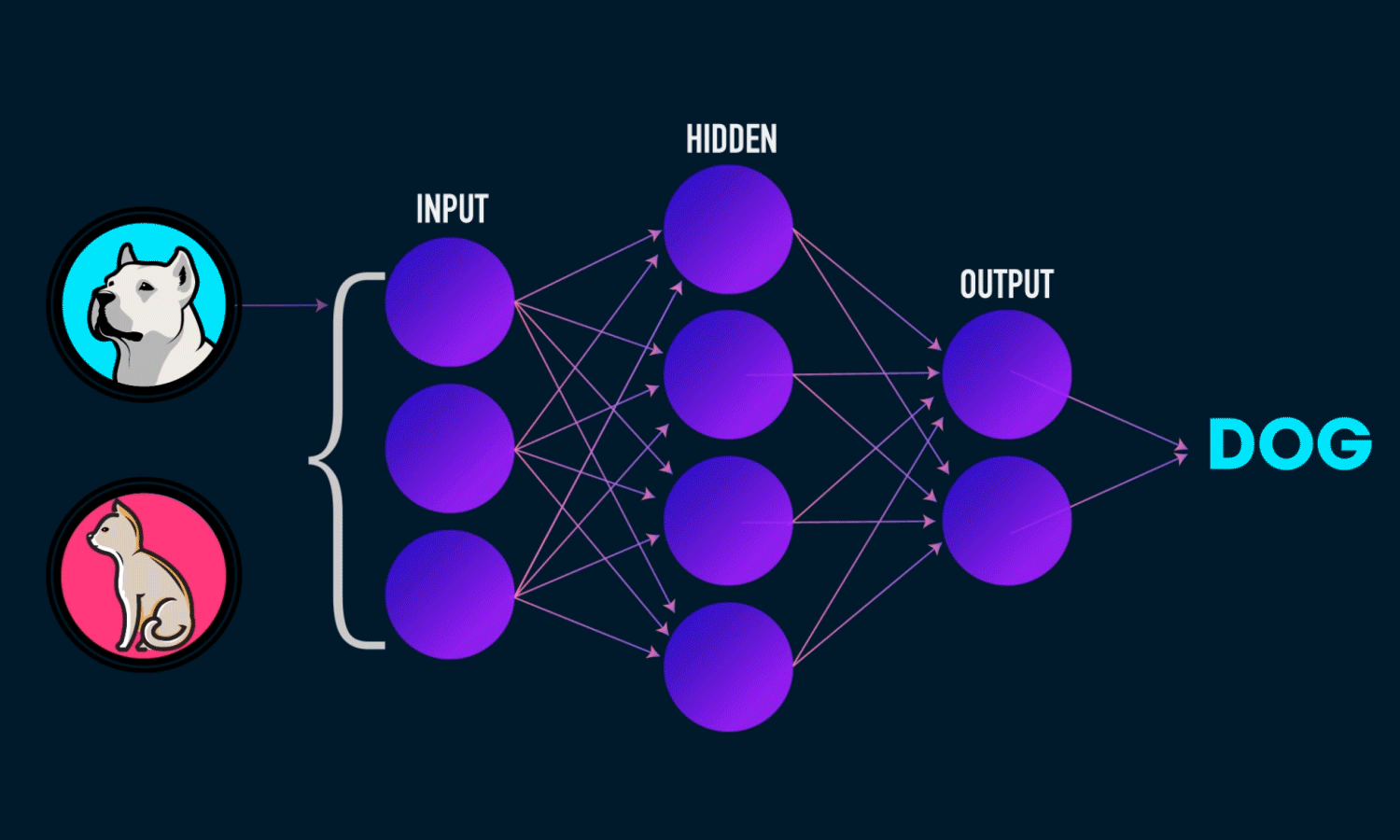
Input Layer: $\mathbf{x}\in{\mathbb R}^n$
Hidden Layer: $\mathbf{W_1}\in{\mathbb R}^{m\times n},\mathbf{b_1}\in{\mathbb R}^m$
Output Layer: $\mathbf{w_2}\in{\mathbb R}^m,\in{\mathbb R}$

隐藏层的维度$m$是一个超参数。

单隐藏层感知机数学表达式为：

\[\mathbf{h}=\sigma(\mathbf{W_1}\mathbf{x}+\mathbf{b_1})\] \[o=\mathbf{w}_2^T\mathbf{h}+b_2\]

其中，$\mathbf{h}$是单隐藏层的输出，$\sigma$ 是按元素的激活函数(activation function)，激活函数必须是非线性的！

如果激活函数为线性：则$o=a\mathbf{w}_2^T\mathbf{W}_1\mathbf{x}+b\prime$仍然是线性的，等于一个单层感知机。也就是说不论深度有多少层的线性感知机，都等价于单层感知机。

常用激活函数
- Sigmoid 函数（多用于二分类问题的 Logistic 回归）
\[sigmoid(x)=\frac{1}{1+e^{-x}}\]
- Tanh 函数
\[tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}\]
- ReLU 函数(Rectified Linear Unit)
\[ReLU(x)=\max(x,0)\]

ReLU 激活函数应用广泛的主要原因是计算简便，求导方便，同时没有指数运算（一次指数运算在 CPU 上相当于上百次乘法运算 😮）

多分类感知机——相当于在 Softmax 回归加入一层隐藏层

\[y_1,y_2,...,y_k=softmax(o_1,o_2,...,o_k)\]

Input Layer: $\mathbf{x}\in{\mathbb R}^n$
Hidden Layer: $\mathbf{W_1}\in{\mathbb R}^{m\times n},\mathbf{b_1}\in{\mathbb R}^m$
Output Layer: $\mathbf{W_2}\in{\mathbb R}^{m\times k},\mathbf{b_2}\in{\mathbb R}^k$
- $\mathbf{h}=\sigma(\mathbf{W_1}\mathbf{x}+\mathbf{b_1})$
- $\mathbf{o}=\mathbf{W}_2^T\mathbf{h}+\mathbf{b_2}$
- $\mathbf{y}=softmax(\mathbf{o})$

以上图网络为例，$n=4,m=5,k=3$

多隐藏层感知机

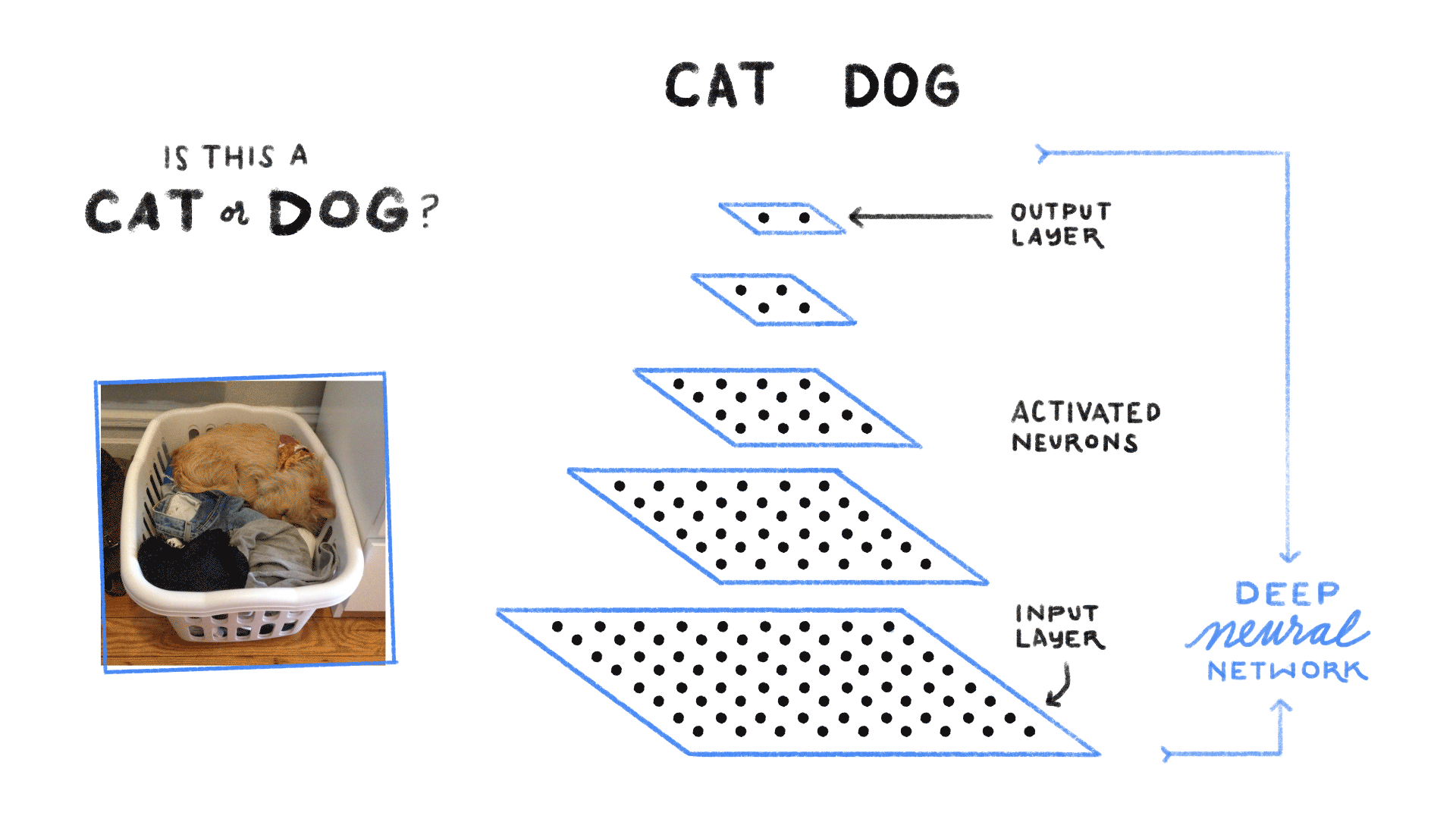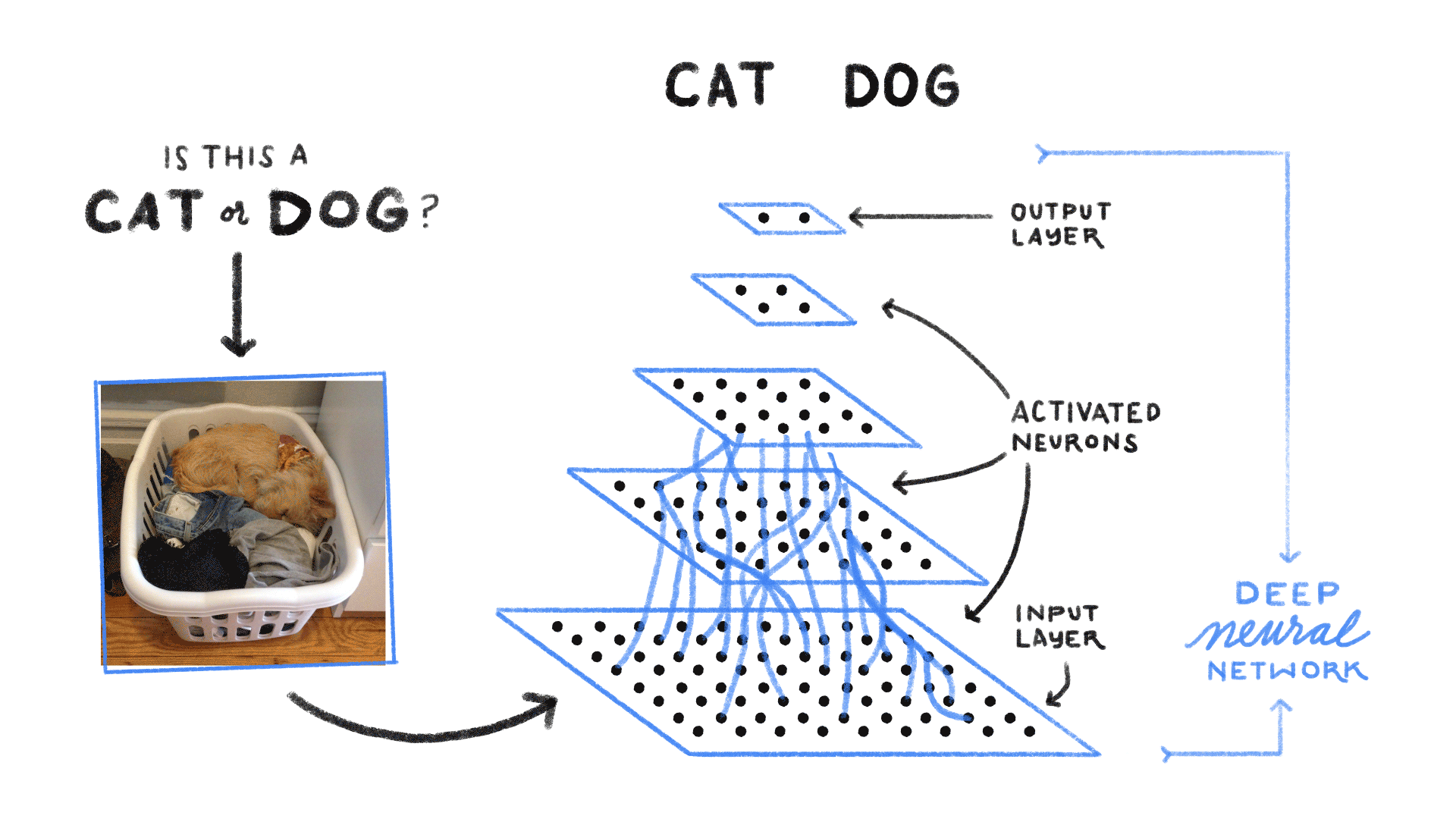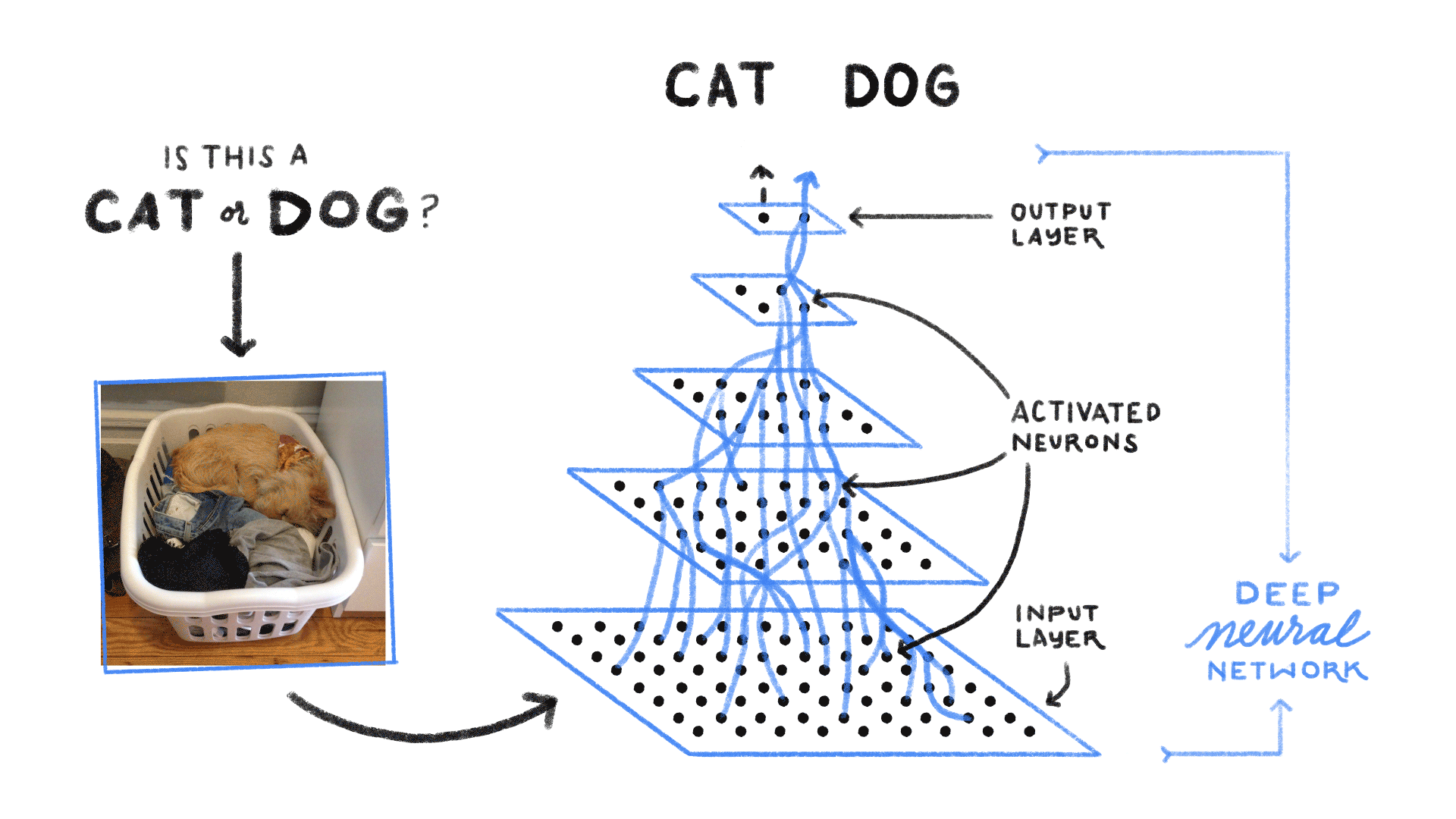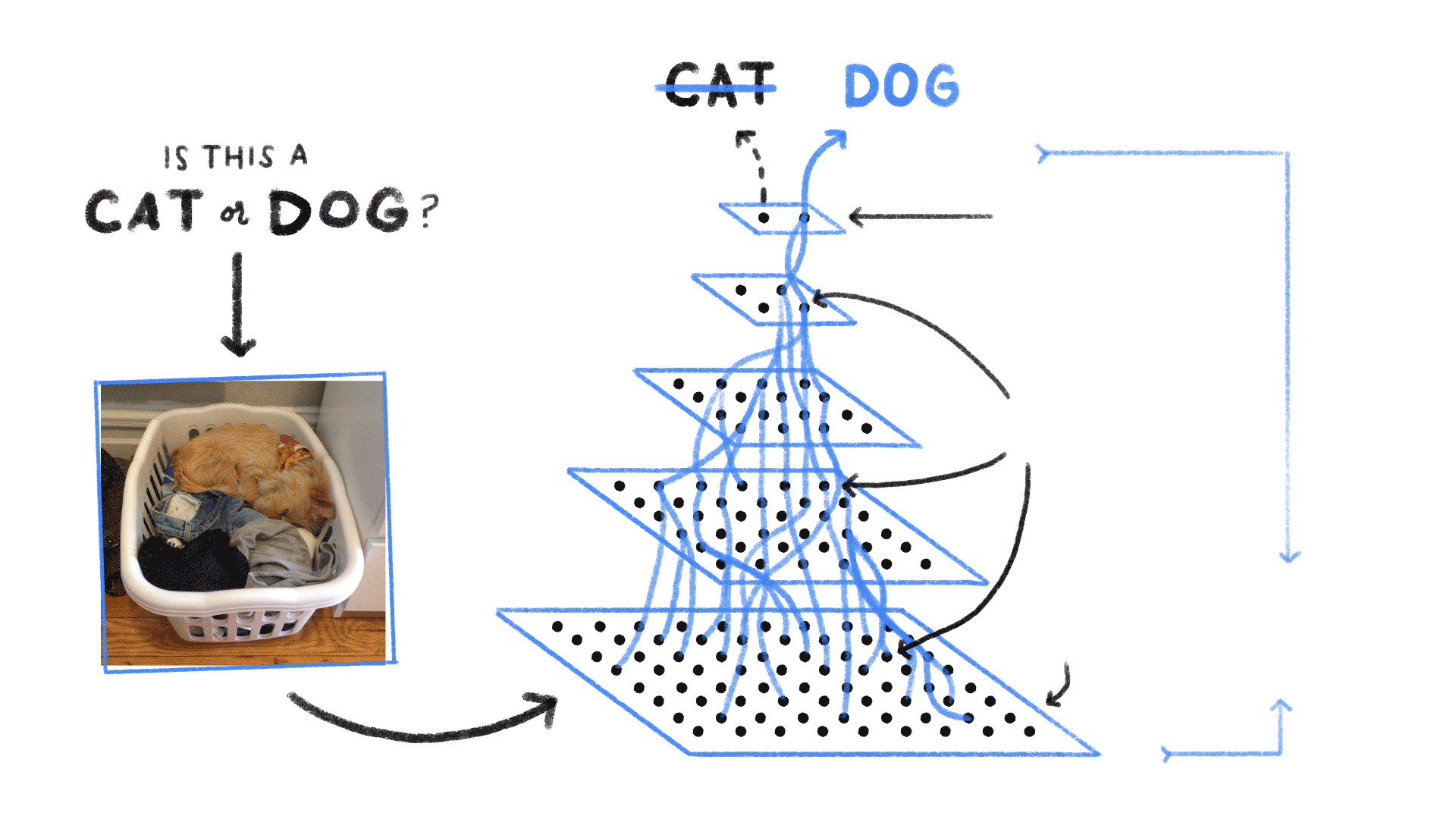
上图卷积神经网络可大致看作是含有三个隐藏层的多层感知机。其中三个激活函数必须均为非线性函数

$\mathbf{h_1}=\sigma(\mathbf{W_1}\mathbf{x}+\mathbf{b_1})$
$\mathbf{h_2}=\sigma(\mathbf{W_2}\mathbf{x}+\mathbf{b_2})$
$\mathbf{h_3}=\sigma(\mathbf{W_3}\mathbf{x}+\mathbf{b_3})$
$\mathbf{o}=\mathbf{W}_4\mathbf{h_3}+\mathbf{b_4}$

超参数：
隐藏层数量 $k$
每层隐藏层的大小$[m_1,m_2,…,m_k]$

一般每个隐藏层大小是逐层递减的，此处一个可解释性是多层感知机相当于对信息做逐层“压缩”，即对知识做蒸馏，Distillation）

多层感知机的代码实现

导入包

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

设置各层参数

一般选用 2 的幂次作为隐藏层数量，因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。
Parameters()指定 input(Tensor)作为模型参数。
torch.randn(m.n)返回符合随机正态分布的 m*n 张量

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

定义 ReLU 激活函数

def relu(X):
    a = torch.zeros_like(X)   #_like(X)表示与输入X的形状相同
    return torch.max(X,a)

定义感知机网络和训练模型

def net(X):
    X = X.reshape(-1, num_inputs)   # X是batch_size*len=256*784
    H = relu(X @ W1 + b1)   # W1=784*256, H=256*256
    return (H @ W2 + b2)    # W2=256*10

loss = nn.CrossEntropyLoss()

训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

简易实现

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0)

net.apply(init_weights);

trainer = torch.optim.SGD(net.parameters(), lr=lr)

num_epochs, lr = 10, 0.1
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

Pytorch 模块参考文档

torch.nn.ReLUPytorch 基本神经网络组件 ReLU 层 🧐中文官方英文

Q&A🤓

Q：如果在模型参数初始化时，对 W 不采用高斯随机分布torch.randn()，而是全零torch.zeros()或全 1torch.ones()分布，会产生什么？

🙋‍♂️：经过实验，对 W、b 采用全零或全 1 初始化，或 W 全零、b 全 1，或 W 全 1、b 全零，模型都无法训练，推测应该是以上四种初始化下，无法计算梯度，则无法进行参数更新。具体原因有待后续讨论。

Q：如果将 ReLU 激活函数换成其他非线性函数，对结果有什么影响？

🙋‍♂️：通过 Benchmark，结果如图：

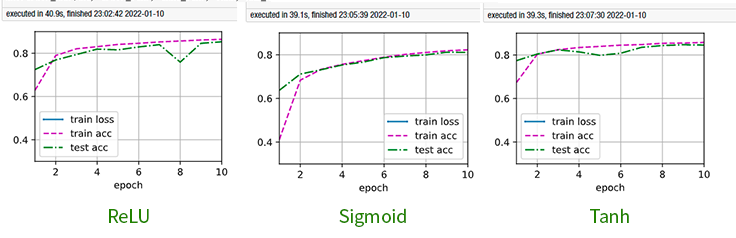
如果换成Sigmoid函数，收敛比 ReLU、Tanh 慢（ReLU 差不多 2 个 Epoch 就基本收敛），训练时间相差不大，精度不如 ReLU、Tanh；
如果换成Tanh函数，收敛速度与 ReLU 相当，训练时间相差不大，精度与 ReLU 相当

Q：如果两个感知机模型复杂度相当，一个是浅层、每层神经元数量多的感知机，另一个是多层、每层神经元数量少的感知机，为什么都倾向于使用后者结构？

🙋‍♂️：理论上来说，这两个模型在激活函数是非线性的情况下，是可以达到相似的精度。根据[Hornik et al., 1989;Cybenko,1989]提出的万能近似定理（universal approximate theorem）表明，单隐藏层的非线性感知机理论上可以拟合任意函数，当然仅是理论上，实际上参数几乎学不出来。但是更深的网络，模型训练起来更容易、收敛更快，浅层网络很难学习。多层感知机解决任务类似于“化整为零、逐个击破”策略。

与之策略类似的是CPU，就是由各种简单功能的元器件（如加法器等等）有机组合在一起而实现复杂功能。

具体原因可以观看吴恩达DeepLearning课程👇《为什么使用深层表示》

Q：上一个问题的答案说非线性感知机理论上可以拟合任何函数，那在函数逼近领域内与另一种方法——傅里叶变换相比，有什么优势使神经网络成为当下主流？

🙋‍♂️：大多数研究表明，傅里叶级数（Fourier Series）是连续函数的通用逼近器。快速傅里叶变换（FFT）可用于从均匀间隔数据中快速计算傅里叶级数。FFT 具有以下特性：如果模型足够光滑，会得到光谱收敛（即连续—离散），这意味着误差呈指数递减（可通过系数的赫尔德条件看出）。而神经网络收敛速度达不到指数级，甚至在最优条件下也很难达到线性收敛速度。

这么看貌似神经网络不如傅里叶变换，但傅里叶变换这种逼近器是一维的，虽然可通过张量积将一维逼近器变为多维，但是这要为更高阶项的每个组合添加新的项，组合以阶乘或近似指数方式增长。例如表示一个 100 维输入的三阶交叉项，需要 161700 个项。这种相对于输入大小呈指数增长的方式是“维度灾难”。而输入大小与神经网络复杂度增长仅是多项式成本。

具体可参考这篇文章（中文）和 Reddit 上的这个帖子（英文）

Yeqi He(贺业祺)

多层感知机

🎦 本节课程视频地址 👇

感知机（Perceptron）

多层感知机(MLP)

单隐藏层——单分类

多分类感知机——相当于在 Softmax 回归加入一层隐藏层

多隐藏层感知机

多层感知机的代码实现

Pytorch 模块参考文档

Q&A🤓

You May Also Enjoy

线性回归

自动求导

矩阵计算

线性代数